Fresnel ellipsoids and line-of-sight

Contrary what you may have learnt in school, light does not travel in straight lines. Any form of electromagnetic radiation such as light and the radio waves can travel along a slightly bent path. Thus, when putting up two antennae, it’s important to have a bit of extra room about the direct line between them in order that the radiation that follows the bent paths can also be transmitted.

The zone that one should try to keep unobstructed is called a Fresnel zone. It’s an ellipsoid, which looks like a highly elongated rugby ball or American football with the antennae at the two tips.

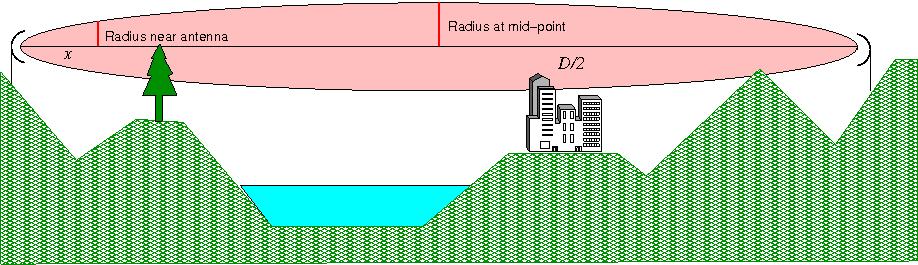
The direct line of sight, or axis, runs from tip to tip. At each point on the axis we want to keep obstructions out of the circle that we’d get if we cut through the football across the axis at that point (and it didn’t deflate!) Half way between the two antennae, the circle can be quite large, so a small obstruction such as a utility pole may not matter that much.

How big are these circles? We’ll give two formulae: one for near the antenna and one for the midpoint of the axis. For any other point else you are safe taking the minimum of these two figures. Read up on Fresnel zones if you want a more detailed analysis.

Midpoint radius

If \(D\) is the distance between the masts and \(\lambda\) is the wavelength, the radius of the ellipsoid at the midpoint is \(1/2\sqrt{\lambda D}\). This means that

• In the 2.4GHz spectrum the radius is about \(0.18\sqrt{D}\)
• In the 5GHz spectrum the radius is about \(0.12\sqrt{D}\)

For example, if you are using 5GHz wireless over a 10km (10,000m) link you should leave 12m clear from the direct line of sight.

Radius near an antenna

Suppose you are a distance \(x\) from an antenna where \(x\) is small compared with the length of the link \(D\). The radius is \(\sqrt{\lambda x}\). This means:

• In the 2.4GHz spectrum the radius is about \(0.35\sqrt{x}\)
• In the 5GHz spectrum the radius is about \(0.25\sqrt{x}\)

For example, at 30m from a 5GHz antenna, the radius is about 1.4m and at 100m it is about 2.5m

Anywhere else

Unless you are keen to read more about Fresnel zones, take the minimum of the two estimates above. For example at 1km from an antenna on a 10km 5GHz link, the radius at the midpoint is 12m and the estimate we get from being “near” an antenna is \(0.25\sqrt{1000}=7.9\)m. So we use the second figure.